中国科普博览-亚博安卓

 太空中的单摆

刘延柱1)

（上海交通大学工程力学系？ 上海？ 200240）

 

摘要 ？讨论太空中的单摆在微重力作用下的摆动规律，计算太空中的单摆周期。论及绳系卫星及舒勒周期摆的摆动。
关键词？ 单摆，微重力，舒勒周期
中图分类号：0313 文献标识码：a
文章编号：

？

今年6月20日，正在太空中翱翔的天宫一号实验室给全国中小学生上了有趣的一堂课。学生们通过电视看到，航天员王亚平演示的单摆在太空中只能绕支点旋转却不能来回摆动（图1）。试想在空间站的失重环境里，所有物体都漂浮在空中，没有往回拉的重力单摆自然就摆不起来。不过再深入做些思考，太空中的单摆也并非完全不能摆动，而是遵循与地面上完全不同的摆动规律。
将空间站的质心作为坐标系的原点，建立与空间站固结的参考坐标系。根据牛顿力学原理，所有相对非惯性坐标系运动的物体除实际作用力以外，还必须增加由于动坐标系的加速度所引起的惯性力。就圆轨道的空间站而言，也就是点圆周运动的离心力。空间站要维持圆周运动，惯性力与地球引力的合力必须大小相等方向相反。地球引力与地心至物体的距离平方成反比。空间站内的不同位置因为与地心的距离和引力不同，重力与惯性力不能完全抵消，就会有“残余”的重力出现。可见重力在空间站里并未完全消失。
？
　　　？？？？？？？？？？？？？？？？？？？？？？？？ ？？
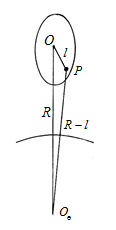
？？？？？？？？？？？？？？？ 图1 天宫一号中的单摆实验　　　　　　　　　？？？？？？？？？？ 图2 太空中的单摆
？
为便于叙述，设空间站的质量作球对称分布。作此规定是因为非球对称物体在中心引力场中的合力作用点不在质心上，叙述较繁但道理相同^[1]。设单摆的悬挂点与点重合，与地心的距离为，单摆的长度为，摆锤指向地心。一般情况下要比大很多，可略去的二次以上小量，则摆锤与地心的距离为（图2）。设点处单位质量的重力为，与单位质量的离心力，即点的向心加速度相等。摆锤处单位质量的重力与之比等于距离平方的反比

　？ 　　　　　　　　　　　　　　(1)

如摆锤的质量为，作用的重力不同于支点加速度引起的惯性力，二者之差形成残余重力，或更确切称之为微重力

　　　　　　　　(2)

既有微重力存在，就应能推动单摆产生摆动。不过推动的动力太微弱，可能产生的摆动极其缓慢。将式(2)代替计算单摆的周期，得到

　　？？？ 　　　　　　　　　　　　　(3)

括号里的是摆长与点至地心距离相等的单摆周期。如果等于地球半径，令，，算出分钟。单摆周期约为的0.7倍，即大约59.7分钟。也就是说，空间站里的单摆需要一个小时才能完成一次摆动。有趣的是在周期公式(3)里，由于分母中的与摆长成正比而与分子中的约去，单摆的周期公式就与摆长无关。这表明伽利略发现的单摆周期随摆长增大的规律在太空中已不再适用。另一个有趣现象是如摆锤不是指向地心，而是背朝地心指向相反方向，则离心力大于重力也同样存在微重力，只是方向相反。因此太空中的单摆不仅朝下，而且朝上也能摆动。
上述周期一小时的单摆摆动现象很难在太空舱内用实验验证。因为推动摆锤的微重力如此之微弱，以致支点摩擦或空气波动的影响都要比微重力的作用大得多。除非摆索的长度加得很长，使微重力的作用增大到足以推动摆锤的程度。这种摆索超长的大单摆在太空中的实际存在就是绳系卫星（图3）。绳系卫星是由作为母星的太空船或空间站以及用系绳悬挂在太空中的子星组成的航天器。子星可朝向地球下垂，也可背向地球上浮。利用绳系卫星可以完成探测、运输甚至发电等特殊任务。上世纪90年代意大利最先研制的绳系卫星实际长度为250m，而设计的长度可达20km。即使系绳如此之长，也远小于地球半径6371km，上述周期的近似计算公式(3)应仍能适用。即无论系绳有多长，也无论子星下垂或上浮，摆动周期均为一小时左右。这种不衰减的摆动可能在子星刚从母星释放后出现，必须采取有效措施对摆动加以抑制，以保证绳系卫星的正常工作^[2]。
公式(3)中出现的摆长等于地球半径的单摆周期分钟有特殊意义。因为1923年德国工程师舒勒(sch ller,m.)曾证明，当支点沿地球表面作任何加速运动时，都不会对这种单摆指向地心的平衡状态产生干扰。文献中将这种周期84.4的特殊单摆称为舒勒周期摆^[3]。尽管在理论上成立，但这种单摆根本无法实现。如将支点放在地球上，摆锤不可能穿透地球到达地球中心。唯一的可能是将支点放在轨道高度超过地球半径的空间站上，半径等于的单摆方有可能摆起来。如支点高度正好等于，使单摆沿地球表面摆动（图4）。由于摆长和地球半径相等，不允许将视为小量，不能再使用近似公式(3)计算单摆的周期。不考虑大气层阻力的影响，由于支点与地心距离是摆锤与地心距离的两倍，则地球引力应相差4倍。即，此处的表示地球表面的重力加速度。则，代入周期公式，得到

　　　　　　　　　　　　　　(4)

由此可见，即使采用这种方案能使摆长等于地球半径的单摆付诸实现，但它的周期已不再是舒勒周期了。
　　　　？？ 　？？？？？？？？？？？？？？？？？？
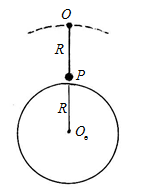
　　　　　　　　？？？ 图3 绳系卫星　　　　　　　？？？？？？？？？？？？？？？？？？？？ 图4 摆长等于地球半径的单摆
？
参考文献
[1]？？？？？？ 刘延柱. 高等动力学. 北京，高等教育出版社， 2001
[2]？？？？？？ 刘延柱. 再谈荡秋千－兼谈自激振动. 力学与实践，2007，29(3)：92-93
[3]？？？？？？ 贾书惠. 神秘的数字84.4. 力学与实践，1997, 19(1): 67-69
？

the simple pendulum in space

liu yanzhu

(dept. engineering mechanics, shanghaijiaotonguniversity, shanghai 200240)

？