|
苏联数学家维诺格拉朵夫(1891-1983),从1934年至1983年一直担任苏联科学院斯捷克洛夫数学研究所的所长。他对韦尔和的估计方法及以素数为变数的指数和估计方法自30年代以来,对数论发展产生了深刻的影响。他在堆垒数论方面得到不少深刻的结果,尤其是他对奇数的哥德巴赫猜想的基本解决及关于华林问题的结论是最为有名。
维诺格拉朵夫的主要成就是发表在30年代,这也是华罗庚进入数论研究的高峰时期。他认真学习了维诺格拉朵夫的方法,虽然华罗庚是自学维诺格拉朵夫方法的。但他对这个方法的了解和贡献却不在旁人之下。维诺格拉朵夫在他的书《数论中的三角和方法》的序言中,提到这个方法是我与柯坡尔特、朱达柯夫、华罗庚及其他人一起合作得出的。
华罗庚最重要的数论工作当然还是他自己独创性的工作。
华氏定理
华氏定理(1940)命q是一个正整数,f(x)=akxk ... a1x
为一个k次整系数多项式且最大公约(ak, ...,a1,q)=1,则对于任何
ε>0皆有
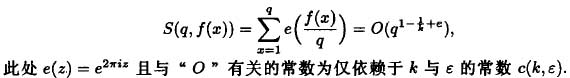
华氏定理溯源于高斯(c.f. gauss)他首先引进f(x)=ax2
的特例情况,
即所谓高斯和: s(q, ax2),(a,q)=1,
并得到估计 s(q, ax2)=o(q1/2 ).
高斯引进并研究高斯和的目的在于给出初等数论中非常重要的二次互反律一个证明。以后,不少数学家企图推广高斯和及他的估计,但他们只能对特殊的多项式所对应的s(q,
f(s)),取得成功,这一历史名题直到1940年,才由华罗庚解决。
华氏定理是臻于至善的,即误差主阶1-1/k 已不能换成一个更小的数。这只是取f(x)=xk 及 q=pk
,p为素数,就可以知道。所以依维诺格拉朵夫称赞华氏定理是惊人的。
华氏定理的直接应用是,可以处理比希尔伯特一华林定理更为广泛的问题:
命n为一个正整数,fi(x)(1<=i <=s )是首项系数为正的k次整值多项式
,
考虑不定方程 n = f1(x1) ... fs(xs)
(1)
的求解问题,特别取f1(x) ... fs(x) =
xk 即得
n =x1k ... xsk .
(2)
1770年,华林提出猜想:当s>=s0(k) , (2)有非零非负整数解
。华林猜想是希尔伯特于1900年证明的。于是华林猜想就成了著名的希尔伯特一华林定理,但用希尔伯特方法所能得到的s0(k)将是很大的
,20年代以后,哈代、李特伍德与依·维诺格拉朵夫用圆法及指数和估计法对s0(k)作了精致的定量估计。用华氏定理基本上可以将依·维诺格拉朵夫关于华林问题的重要结果推广至不定方程(1), 即假定(1)满足必须满足的条件,则当s>=s0 =o(klog k)及n充分大时,
(1)有非零非负整解。当 s >= s0'=o(k2log k) 时
,方程(1)的解数有一个渐近公式。
华氏不等式
华氏不等式(1938)命n 为一个正整数,f(x)为一个k次整系数多项式,则
t(a)=∑x=1ne(af(x)),
则对于任何ε>0及1<=j<=k
时皆有
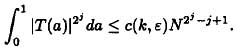
华氏不等式的直接应用为不定方程(1),由圆法来处理方程(1),则首先需将方程(1)的解数表示成(0,1), 上的一个积分
,然后将(0,1)分成互不相交的优孤与劣孤之并, 优孤上的积分给出(1)的解数的主项,需证明劣孤上的积分是一个低阶项
,从而可以忽略不计,这样就得到了解数渐近公式。华罗庚证明了fi(x)(1<=i<=s)假定。为满足必须满足的条件的k次整值多项式
,则当s >= 2k 1 时,方程(1)的解数有一个渐近公式。特别对于华林问题,即方程(2),当s >=
2k 1 时,对充分大的n,有非寻常非负解,且解数有渐近公式。当k <=10时,这一结果是华林问题的最佳结果
。直到半个世纪之后,基于对华氏不等式的某些改良,沃恩(r.f.vaughan)与希斯布朗(d.r. heath-brown )才能对华罗庚关于华林问题的结果作点改进,但他们所用的方法却繁得多了。
基于华罗庚关于解析数论的基本方法,即关于指数和估计的华氏定理与华氏不等式,再加上依· 维诺格拉朵夫的韦尔
(h. weyl)和估计与关于素数变数的指数和估计,华罗庚系统地研究了不定方程及其他堆垒问题的求解问题,并限制变数 x1,x2,...xs均取素数值。华罗庚的结果总结在他的专著《堆垒素数论》中,这本书被译成俄文、英文、德文、匈牙利文与日文,它是圆法、指数和估计及其应用方面最重要的经典著作之一
。 |

